Séparation à contre courant

Séparation à contre courant

Introduction :

Elle fait appel au partage entre deux solvants non miscibles, à la différence des méthodes d’extractions qui permettent l’extraction quantitative d’un composé, la méthode de Craig permet la séparation de plusieurs substances initialement présentes dans une solution, grâce à la différence des coefficients de partage des diverses substances.

A- Principe :

La séparation à contre courant a été mise au point par CRAIG (1950).

Elle est basée sur la répartition d’une substance entre deux phases liquides non miscibles, ce qui permet de séparer les constituants dissous dans une phase initiale en les rassemblant dans des fractions distinctes de solvants.

La séparation est possible, si pour des solvants choisis, les substances ont des coefficients de partage différents.

𝐾_𝐷 =

A

A

[𝐴]𝑜𝑟𝑔 [𝐴]_𝑎𝑞

Figure 1 : Partage d’une substance entre deux solvants non miscibles

B- Appareil de CRAIG :

Description : Il se composé de deux blocs, l’un inférieur et l’autre supérieur.

Bloc inférieur cylindrique creusé de 20 cavités, dans lesquelles sont disposés des tubes de capacité identique.

Ils sont numérotés de 0 à 19 et sont destinés à recevoir le même volume du solvant lourd.

Bloc supérieur mobile, qui s’adapte sur le précèdent.

Il est également creusé de 20 cavités numérotées de 0 à 19 dans le sens inverse de celui du bloc inférieur.

Toutes les cavités supérieures sont identiques et destinées à recevoir le même volume du solvant léger.

Les deux blocs sont ajustables de manière hermétique, chaque tube inférieur est en communication avec un tube supérieur.

L’ensemble de deux tubes constitue une colonne.

Fonctionnement :

On suppose que la solution contenant la substance à séparer est la phase lourde.

Le tube inférieur N₀ est rempli avec cette solution, tous les autres tubes du bloc inférieur sont remplis avec le même volume du solvant lourd pur.

Le cylindre supérieur mobile est ajusté de telle sorte que les deux tubes supérieurs et inférieur N₀ soient superposés, un même volume du solvant léger pur est introduit dans chacun des tubes supérieurs.

L’appareil est agité énergiquement par retournement, suivi d’un repos destiné à réaliser la décantation des deux phases dans chaque colonne verticale.

Le cylindre mobile est soumis à une rotation vers la gauche de façon à ce que les ménisques de séparation coïncident exactement avec le plan de rotation, séparant ainsi les deux phases.

L’ensemble (agitation + rotation) constitue une opération

Les opérations suivantes sont effectuées de manière identique jusqu’à ce que le tube fixe N₀ coïncide avec le tube mobile N_(n-i).

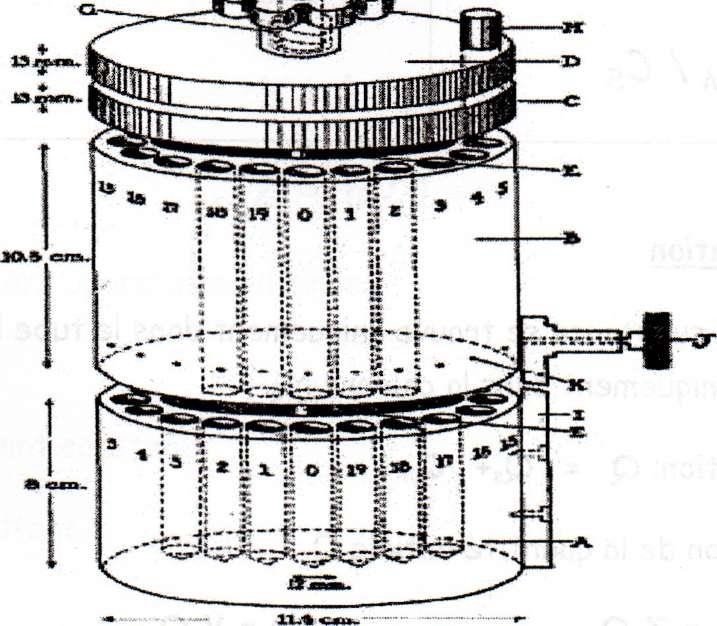
Figure 2 : Schéma représentatif de l’appareil de Craig

C- Etude quantitative pour une distribution régulière :

Au cours de l’agitation, dans chaque colonne, où se trouvent des substances, il y a répartition de celles-ci entre les deux phases en fonction de leurs coefficients de partage.

Si l’agitation est suffisante l’équilibre est atteint.

Notation :

Indice S (stable) : solvant lourd contenu dans le cylindre inférieur.

Indice M (mobile) : solvant léger contenu dans le cylindre supérieur.

Indices A, B, C, … : substances dissoutes.

Equations :

Comme pour l’étude des diverses méthodes d’extraction, les deux équations mises en œuvre sont :

Equations de partage : 𝐷 = ∑𝐶𝑀

𝜆 = 𝐶𝑀

𝛼 = 𝑄𝑀 = 𝜆 𝑉𝑀

∑𝐶𝑆

𝐶𝑠

𝑄𝑆

𝑉𝑠

Equation de conservation de la matière : Q = ΣQ_M + ΣQ_S

Expressions du partage par opération :

Première opération :

Avant agitation, la substance se trouve uniquement dans le tube inférieur N₀.

Le partage se fait uniquement dans la colonne N₀.

Après agitation: Q = Q_M + Q_S

Q_M et Q_S étant les fractions de la quantité initiale Q.

Q_M = ZQ Q_S = YQ

Z et Y : fractions dont la somme égale à 1.

Q = Q_M + Q_S => Q = ZQ + YQ => Z + Y = 1

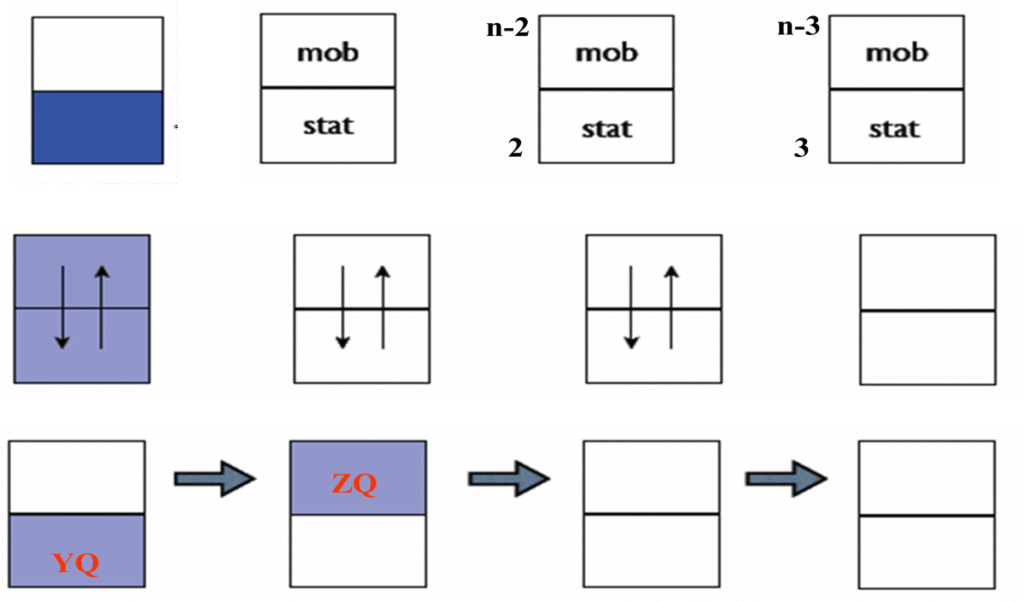
Figure 3 : Schéma de la première opération

Calcul des fractions Z et Y :

𝛼 = 𝑄𝑀

𝑄𝑆

=> 𝛼 = ZQ YQ

=> 𝛼 = Z Y

=> Z = αY

Z + Y = 1 => (α + 1)Y = 1

On obtient : 𝐘 = 𝟏

𝛂+𝟏

et 𝐙 = 𝛂

𝛂+𝟏

Dans des conditions opératoires données :

V_M et V_S sont constants.

D est constant.

Il en résulte que Y et Z sont constants tout au long des diverses opérations et indépendants de la quantité Q.

Ils seront donc utilisés pour l’étude quantitative des opérations suivantes.

Deuxième opération :

Initialement, la substance se trouve repartie dans deux colonnes 0 et 1 (tubes fixes).

L’agitation réalise un équilibre dans chaque colonne en respectant une répartition selon les fractions Y et Z dans chaque cas.

Le partage se fait dans les colonnes N₀ et N₁ :

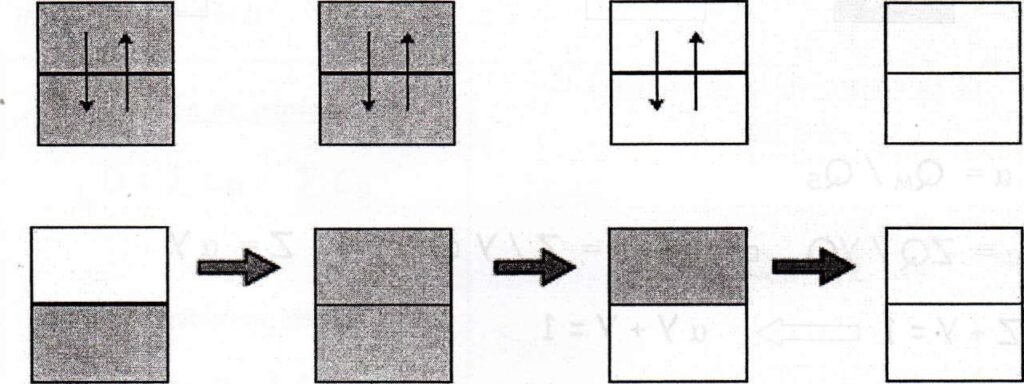
Figure 4 : Schéma de la deuxième opération

– Après agitation :

Colonne 0 : YQ = Y(QM + QS)	=>	YQ = YQM + YQS =>	YQ = YZQ + Y2Q
Colonne 1 : ZQ = Z(QM + QS)	=>	ZQ = ZQM + ZQS =>	ZQ = Z 2 Q + ZYQ

– Après rotation : répartition de Q dans trois colonnes.

 Colonne 0 : Y²Q  Colonne 1 : 2YZQ  Colonne 2 : Z²Q

=> Q = Y²Q + 2YZQ + Z²Q => Q = (Z + Y)²Q

Troisième opération :

Initialement, la substance se trouve repartie dans trois colonnes 0, 1 et 2 (tubes fixes).

Le partage se fait dans les colonnes N₀, N₁ et N₂ :

Après agitation :

 Colonne 0 : Y²Q = Y²Q_M + Y²Q_S => Y²Q = Y³Q + ZY²Q

 Colonne 1 : 2ZYQ = 2ZYQ_M + 2ZYQ_S => 2YZQ = 2Y²ZQ + 2YZ²Q  Colonne 2 : Z²Q = Z²Q_M + Z²Q_S => Z²Q = YZ²Q + Z³Q

Après rotation : répartition de Q dans quatre colonnes.

 Colonne 0 : Y³Q  Colonne 1 : 3Y²ZQ

 Colonne 2 : 3YZ²Q  Colonne 3 : Z³Q

=> Q = Y³Q + 3Y²ZQ + 3YZ²Q + Z³Q => Q = (Y + Z)³Q

Expression générale du partage (n^e opération) :

Première opération : Q = (Y + Z)¹Q

Deuxième opération : Q = (Y + Z)²Q

Troisième opération : Q = (Y + Z)³Q

On remarque que la substance se repartit selon une distribution binomiale.

Un raisonnement par récurrence peut être appliqué pour n opérations :

Q = (Y + Z)ⁿQ

D- Interprétation analytique :

Le raisonnement mathématique montre que toutes les colonnes contiennent une fraction de la quantité initiale Q avec une différence significative des quantités contenues dans chaque colonne.

Influence du rang de la colonne :

Z et Y sont inférieurs à 1 et les valeurs de Yⁿ et Zⁿ sont d’autant plus petits que n augmente.

Donc plus le nombre d’opérations augmente, plus les quantités existantes dans les colonnes extrêmes sont faibles.

Au bout d’un nombre important d’opérations et pour des concentrations initiales de l’ordre du mole/L, on peut atteindre des valeurs d’Yⁿ et Zⁿ inférieures à 1/N (nombre d’Avogadro).

La quantité présente dans de telles colonnes est nulle.

D’autre part, l’un des termes de l’équation binominale correspond à une présence réelle de substance et est plus grand que les autres.

La colonne correspondant à ce terme contient donc la plus grande quantité de substance.

Représentation graphique :

Pour un nombre d’opérations n fixe, on peut tracer la courbe donnant la fraction de la quantité initiale Q de la substance en fonction des rangs de la colonne.

La courbe dépend des valeurs de Z, Y, D, V_M et V_S.

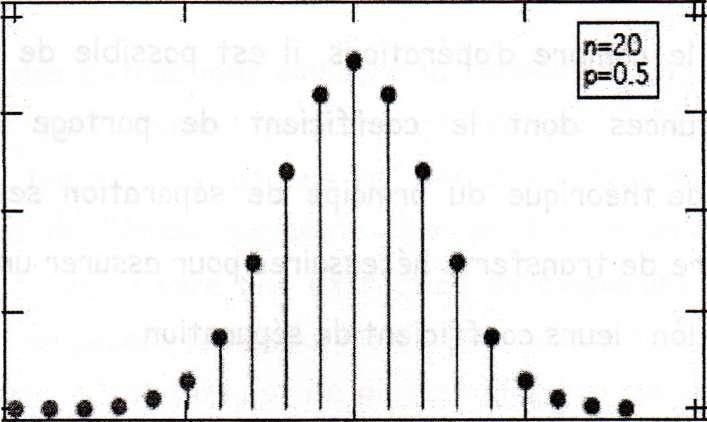
Figure 5 : Représentation graphique de la distribution de Craig

Tableau : Séparation de deux substances de coefficients de partage différents Nombre d’opérations = 08

Nbr. d’opérations (n)	Terme du binôme ou rang de colonnes (tubes supérieurs)
	0	1	2	3	4	5	6	7	8
0	1
1	Z	Y
2	Z2	2ZY	Y2
3	Z3	3Z2Y	3ZY2	Y3
4	Z4	4Z3Y	6Z2Y2	4ZY3	Y4
5	Z5	5Z4Y	10Z3Y2	10Z2Y3	5ZY4	Y5
6	Z6	6Z5Y	15Z4Y2	20Z3Y3	15Z2Y4	6ZY5	Y6
7	Z7	7Z6Y	21Z5Y2	35Z4Y3	35Z3Y4	21Z2Y5	7ZY6	Y7
8	Z8	8Z7Y	28Z6Y2	56Z5Y3	70Z4Y4	56Z3Y5	28Z2Y6	8ZY7	Y8

E- Intérêt de la méthode de Craig :

En augmentant le nombre d’opérations, il est possible de séparer totalement plusieurs substances dont les coefficients de partage sont suffisamment différents.

L’étude théorique du principe de séparation selon Craig permet de prévoir le nombre de transferts nécessaires pour assurer une bonne séparation des espèces selon leurs coefficients de séparation.