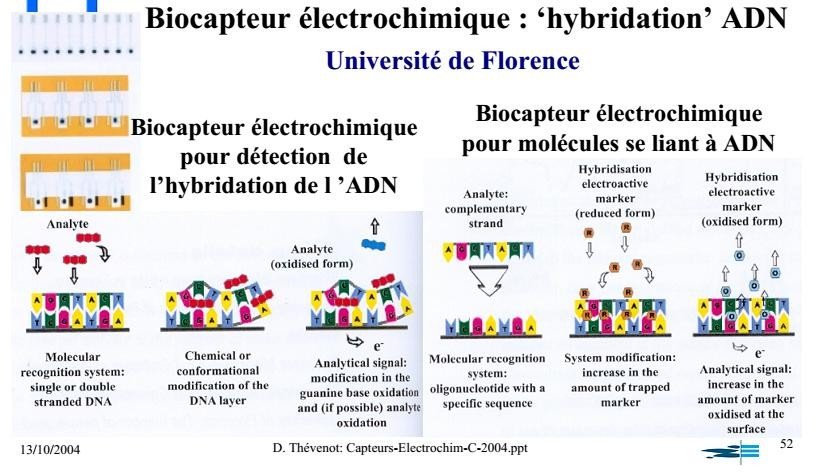
METHODES ELECTROCHIMIQUES – Chimie Analytique Fondamentale
VI-4- Méthodes d’analyses électrochimiques VI-4-1- potentiométrie
La potentiométrie est une méthode qui mesure la différence de potentiel entre une électrode plongeant dans la solution à analyser et une électrode de référence ayant un potentiel fixe et connu (ce qui constitue une demi-pile électrochimique).
Le potentiel de l’électrode de mesure est relié à la concentration de l’espèce en solution par la loi de Nernst.
Montage d’un dosage potentiométrique
la chaîne électrochimique de ce dosage est la suivante :
Électrode de référence | Jonction| Analyte | Électrode Indicatrice
Le potentiel (ou tension de cellule) mesuré sera donné par l’équation :
U = Eind – Eréf + Ej
Exemple : Dosage potentiométrique : Fe2+ par MnO4-
On cherche à mesurer la concentration C0 d’une solution
aqueuse contenant du Fer (II):
FeSO4 → Fe2+ + SO42-.
Pour cela, on réalise un dosage avec du permanganate de potassium:
KMnO4 → K+ + MnO4− de concentration connue C = 2.10-2 mol/L.
Le pH sera maintenu constamment proche de 0, pour éviter que n’interviennent d’autres types de réactions.
On a besoin de deux électrodes pour suivre le potentiel de la solution :
– Electrode indicatrice de Platine (Pt) pour lire le potentiel de la solution
– Electrode de référence (2ème espèce) : potentiel fixe (Electrode au
calomel saturé, ou au sulfate mercureux par exemple
1/ Equation du dosage :

2/ Tableau d’avancement et évolutions

1/Avant l’équivalence : MnO4- versée, le couple redox Fe3+/Fe2+ s’établit : Coté lecture : Elu = EFe3+/Fe2+ – Eréf avec: Eréf = 0,244 V pour l’électrode au calomel (Hg2Cl2).
Par ailleurs, le potentiel d’électrode: EFe3+/Fe2+ = E0Fe3+/Fe2+ + 0.059 log ([Fe3+]/[Fe2+])
2/ A la demie équivalence: V1/2eq = Ve/2 on a [Fe2+] = [Fe3+] Le potentiel d’électrode : E1/2eq = EPt = E0
Fe3+/Fe2+
Ou Elu = E0Fe3+/Fe2+ – Eréf D’où la valeur de E0Fe3+/Fe2+
3/ A la double équivalence : V2eq = 2Veq, [MnO4-] = [Mn2+]
Le potentiel est :
Elu = E0MnO4-/Mn2+ + (0.059/5) log ([MnO4-][H3O]8/[Mn2+]) – Eréf Elu = E0MnO4-/Mn2+ + (0.059/5) log ([H3O]8) – Eré
D’où la valeur de E0MnO4-/Mn2+ E2eq ≈ E0MnO4-/Mn2+ – 0.1 pH – Eré
4/ A l’équivalence : nFe2+ = 5nMnO4-, les deux couples cohabitent dans la même solution
– EFe3+/Fe2+ = E0Fe3+/Fe2+ + 0.059 log [Fe3+]/[Fe2+]
– E MnO4-/Mn2+ = E0MnO4-/Mn2+ + (0.059/5) log ([MnO4 ][H3O]8/[Mn2+])
La Somme des deux équations
0 0
Eeq = (E + 5E )/6
Fe3+/Fe2+ MnO4-/Mn2+
En générale :
Eeq = (n1E0 + n2E0 )/(n1 + n2)
1
2
5/ Après l’équivalence : C’est le couple MnO4-/Mn2+ qui contrôle le potentiel
Elu = E0MnO4-/Mn2+ + (0.059/5) log ([MnO4-][H3O]8/[Mn2+]) – Eréf
1.38V
Dosage potentiométrique du fer(II) par le permanganate de potassium
Ampérométrie
voltampérométrie
La connaissance des caractéristiques fondamentales d’une réaction électrochimique se fait au moyen de la mesure des variations du courant en fonction du potentiel appliqué aux bornes d’une cellule d’électrolyse.
La détermination expérimentale de la relation entre le courant et le potentiel d’électrode se traduit par l’obtention de figures appelées voltampérogrammes.
Elle est l’objet de la voltampérométrie.
Pour une même réaction, la forme de la réponse voltamétriques dépend d’un facteur essentiel qui est le régime de transport diffusionnel des espèces électroactives en solution, régime déterminé par les modalités instrumentales employées.
Les applications analytiques des techniques voltampérométriques sont exposées aux cas de:
l’étude thermodynamique des réactions en solution ;
l’étude cinétique des mécanismes réactionnels couplés au transfert électronique ;
l’étude des phénomènes d’adsorption.
Le système à trois électrodes est le plus utilisé comme le montre la figure ci-après :
Courbes i=f(E) Montage
Electrode de
V référence A
Electrode indicatrice
i = 0
Contre électrode ou auxiliaire
Tableau préliminaire
| Espèces présentes dans le bécher | VCe =0 | VCe <Ve | VCe =Ve | VCe >Ve |
| Réducteurs: i(anodique) | Fe2+ | Fe2+ Ce3+ | Ce3+ | Ce3+ |
| Oxydants: i(cathodique) | Fe3+ | Fe3+ | Fe3+Ce4+ |
) ) )
| Bilan courants | i(anodique) | i(anodique)i(cathodique | i(anodique)i(cathodique | i(anodique)i(cathodique |
Courbes intensité potentiel
I
Ce4+
V=0
Fe2+ Fe3+
V<Ve
V=Ve
V>Ve
Fe2+
Ce3+
Ce3+
E2
E1
Ce4+
E
Ce4+
Fe2+ Fe3+
i=f(E) cas d’un réducteur
I
ia
Red Ox
Vague anodique ia = k[Red]
E
Red
i=f(E) cas d’un oxydant
I
Ox
E
Red Ox
Vague cathodique
i
c
ic = k[ox]
Polarographie
Le principe de la polarographie consiste à tracer des courbes voltampérométrique d’une solution en utilisant une micro-électrode à goutte de mercure.
Voltampérométrique revient à parler des courbes intensité-potentiel i=f(E).
Donc toujours ici 2 électrodes et un circuit électrique avec un potentiomètre (on peut aussi avoir des montages à 3 électrodes).
Dans le circuit électrique, on a un milliampèremètre (µA), un millivoltmètre (V) car les courants qui passent dans le circuit ne sont pas très élevés puisque l’on cherche à faire une micro- électrolyse.
Ce circuit est alimenté par une pile et l’espèce de ressort montre que c’est un potentiomètre variable.
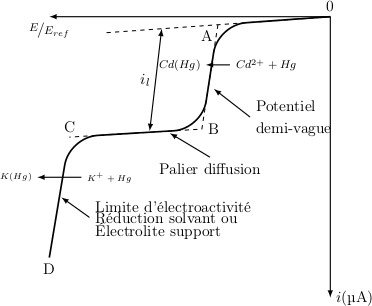
Le polarogramme est l’exploitation des courbes intensité-potentiel.
On a appris que lorsque l’on augmentait le courant, l’intensité augmentait, mais il faut savoir qu’il y a toujours des impuretés dans les solutions donc on a toujours au début un courant résiduel.
Ensuite on a formation d’une goutte qui tombe et ainsi de suite, donc on obtient un tracé en zigzag et l’on trace le courant moyen (courbe).
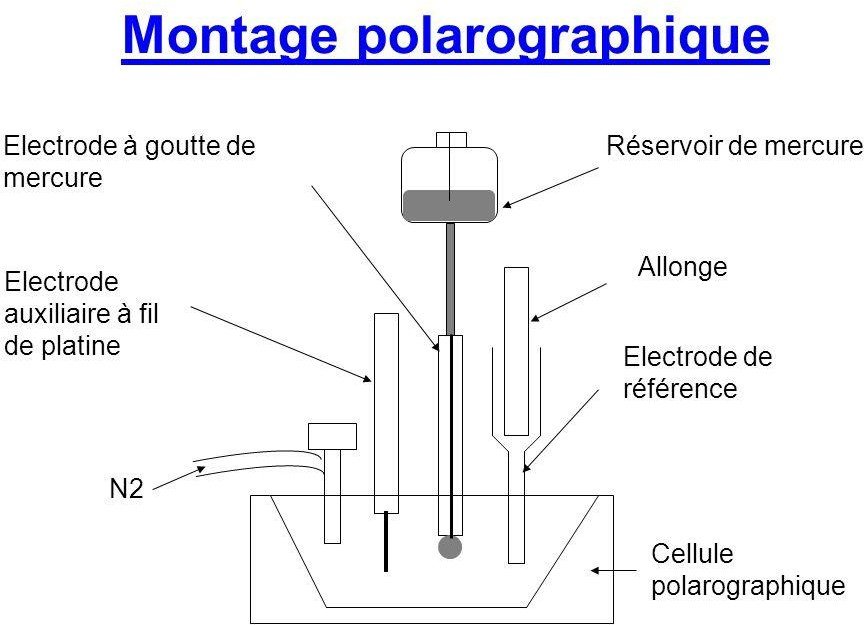
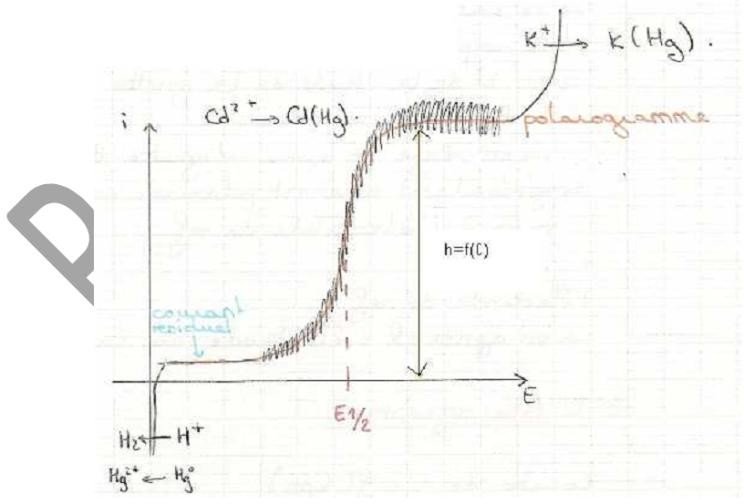
Le polarogramme peut être caractérisé par le potentiel de ½ vague, et l’on a la hauteur (h) qui est proportionnelle à la concentration.
Donc pour faire les dosages, on pourra faire une courbe étalon, cela veut dire que l’on pourra avoir une idée de la concentration de la substance à doser par rapport à la hauteur du palier (h).
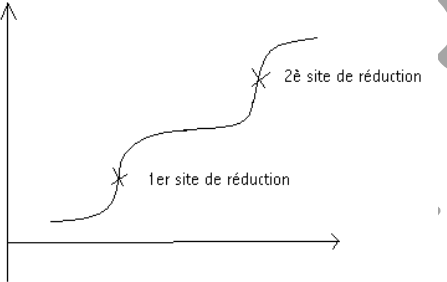
Les substances dosables par polarographies sont les cations minéraux,
mais aussi on peut polarographier des substances organiques.
Certaines substances organiques auront plusieurs sites de réduction dans la molécule qui donneront des tracés avec plusieurs sites de réductions, cela permet de voir quel est le comportement de certaines molécules.
Potentiel
Intensité de courant
L’intensité du courant moyen est déterminée par l’équation d’ILKOVIC.
On va se servir de la loi de Fick, en tenant compte de la surface de l’électrode et du temps de vie de la goutte pour obtenir finalement l’intensité id du courant moyen.
id = 607. n . m2/3 .
D01/2 . τ1/6 .
Cs
n : nombre d’électrons échangés
m : masse de Hg en mg qui s’écoule par seconde Cs : mmole/L
τ : période de la goutte
On arrive au fait que l’intensité du courant moyen est proportionnelle à la concentration de l’espèce électroactive.
A partir de la hauteur des vagues déterminées dans les deux mesures successives, il est facile de déterminer la concentration de la substance à doser.
L’inconvénient de cette méthode réside dans le fait que le composé à doser peut contenir de nombreux ions non électroactif qui vont modifier les propriétés physiques de la solution et de l’électrode
à goutte de mercure.
C’est pour cela qu’on procède à l’une des deux méthodes
suivantes:
1/ méthode de l’ajout dosé
2/ technique de l’étalon interne
1/ Méthode de l’ajout dosé
On prépare une solution de concentration C de la substance à dosé
Soit un volume V(mL) de la solution à dosé de concentration C inconnue dans le quel
On ajoute un volume A(mL) d’eau distillée dont la concentration de la substance
Cs = VC/(V+A) , la mesure polarographique donne une intensité I1
-A un volume V(mL) de la solution à dosé de concentration C inconnue on ajoute un volume A(mL) d’une solution étalon de concentration Ce
Cs = (VC + ACe)/(V+A), la mesure polarographique donne une intensité I2
Les rapports des intensités de courant d’après la relation d’ILKOVIC
(I2/I1)= (VC + ACe)/VC donc la concentration cherchée
C = (ACeI1)/V(I2-I1)
2/ technique de l’étalon interne
Cette méthode consiste à ajouter un ion différent de celui qu’on veut doser, cet ion
pilote présente une vague connue.
Il suffit de déterminer les rapports des hauteurs de vagues Obtenues respectivement pour la substance à doser et l’ion pilote.
D’près ILKOVIC le rapport des intensités de courant de diffusion est égale au rapport des coefficients de diffusion DA, DB à la puissance ½ de ces deux ions
Si les concentrations et le nombre d’électron sont égaux
IA/IB = DA1/2/DB1/2 = KAB
Soit les concentrations CA et CB les concentrations de A et B
IA/IB = (DA1/2/DB1/2 ) CA/CB= KAB (CA/CB)
Donc, il est possible de déterminer la constante relative KAB correspondant au rapport des coefficients de diffusion grâce à deux mesures d’intensités
Sur deux solutions de chaque ion à concentration connue
Si, dans une solution de composé B de concentration inconnue CB, on ajoute le composé A à
une concentration connue CA .
On enregistre les deux vagues sur le même polarogramme.
Le rapport des intensités est directement proportionnel au rapport des concentrations
CB = KAB CA IB/IA
Les résultats donnés par cette méthode sont excellents à condition que les deux vagues soient suffisamment différents
Ampérométrie
Dans l’ampérométrie, on trace des courbes i = f(C) en fixant le potentiel E, c’est une méthode qui découle de la voltampérométrie.
Pour la mettre en œuvre, on utilise toujours les courbes intensité-potentiel, donc même chose si l’on veut doser du cadmium, on va tracer la courbe intensité-potentiel.
Exemple du Plomb :
Pb2+ + SO 2- → PbSO ↓
4 4
Si on veut doser du plomb en ampérométrie, on va doser Pb2+avec des ions SO
2-de
4
manière à obtenir un précipité de PbSO4.
Ici le plomb sera la substance
électroactive et SO 2- ne sera pas électroactif dans les conditions de la réaction.
La
4
grande différence avec la polarographie, c’est que l’on se place à un potentiel E.
Au
fur et à mesure que le réactif SO 2- est ajouté, la concentration en plomb va
4
diminuer.
On a les ions qui migrent entrent les 2 électrodes avec les ions qui correspondent à l’électrolyte support qui servent au transport des charges.
Mais le courant qui sera surtout utilisé est le courant de diffusion.
Le courant de diffusion moyen sera calculé en se servant de l’équation classique du courant de diffusion :
i = k (Cs-Ce) ; où Cs et Ce sont les concentrations au sein de la solution et sur l’électrode respectivement et on tient compte en plus de la loi de Fick : déplacement des ions dans les milieux en fonction de la viscosité :
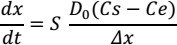
S : surface de l’électrode
D0 : coefficient de diffusion caractéristique de l’espèce électrolysée (cm2/s)
∆x : épaisseur de la couche de diffusion
L’intérêt de l’ampérométrie est que l’on se fixe à un potentiel E, mais l’on n’est pas obligé de tracer toutes les courbes, on va donc tracer i=f(C), et donc on reporte i4 qui est l’intensité la plus importante et ensuite au fur et à mesure que l’on ajoute SO42-, Pb2+étant électroactif
et SO42- non électroactif, on aura une baisse de l’intensité i.
Au point
d’équivalence, on a un tracé relativement plat correspondant au courant résiduel.
En résumé, En polarographie, on fait varier le potentiel (un balayage de potentiel), tandis qu’en ampérométrie on fixe le potentiel E sur le palier de diffusion
i i
i4 i4
i3 i3
i2 i2
i1 i1
Eimp E
Point équivalent
Vajouté
Les dosages à une électrode indicatrice et une électrode de référence: Dans ce cas, on réalise un montage à trois électrodes (référence, indicatrice et auxiliaire), et on impose des potentiels tels qu’aucun courant ne passe dans l’électrode de référence, et que le potentiel de l’indicatrice soit fixé par rapport à celui de la référence ; on mesure alors le courant traversé par l’électrode indicatrice au cours du dosage.
Les dosages à deux électrodes indicatrices: Dans ce cas, on réalise un montage à deux électrodes seulement, le courant passant dans les deux, et la différence de potentiel entre les deux étant fixé.
Le courant d’électrolyse doit être suffisamment faible (quelques µA) pour ne pas modifier la concentration de l’espèce à doser.
Courbes intensité-potentiel correspondant au dosage des ions Ce4+ par les ions Fe2+
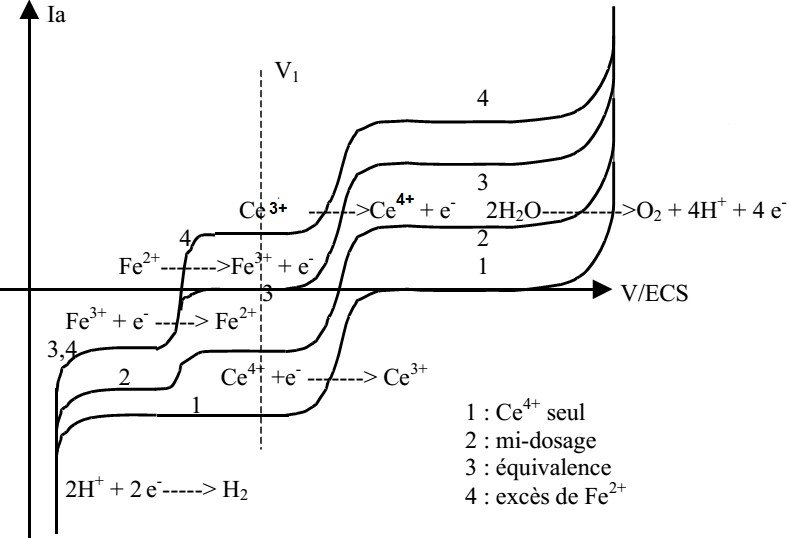
Courbes intensité-potentiel lors du dosage d’une solution d’ions cériques par les ions ferreux (Ce4+ + Fe2+ Ce3+ + Fe3+ ).

La potentiométrie à tension
imposée Ampérométrie
Type de courbes selon le choix des électrodes:
Référence + Indicatrice :
i i i
(a) V
(b) V
i
espèce titrée est électroactive
espèce titrante est électroactive
les deux espèces sont électroactives (deux oxydations ou deux réductions)
les deux espèces sont électroactives (Une oxydation et une réductions)
(c) V
V
(d)
Coulométrie
En coulométrie, on utilise toujours des courbes intensité-potentiel, mais ce n’est pas une méthode indicatrice, c’est une méthode qui va consommer la totalité de la substance à doser.
Introduction
La coulométrie est une méthode d’analyse basée sur la mesure d’une quantité d’électricité.
Cette quantité d’électricité va être mise en jeux au cours d’une réaction, comme par exemple une réaction classique :
Ox + ne- ↔ Red
Fe3+ + 1e- ↔ Fe2+
Pour réduire une mole de Fe3+, il faudra une mole d’électrons.
C’est une quantité d’électricité correspondant à une mole d’électrons, qui s’appelle encore un Faraday : F = N.e- (avec N : nombre d’avogadro, et e- : charge élémentaire d’un électron) 1 F = 96500 coulomb.
Le Coulomb est la quantité d’électricité traversant un conducteur parcouru par un courant de 1 ampère pendant une seconde.
Q = i x t (Q : en coulomb C, i : en ampère A, t : en secondes s) L’intérêt de la coulométrie est que l’on n’a pas besoin d’utiliser de solution titrée puisque le coulomb est lui-même l’étalon.
Par rapport à la volumétrie classique, l’intensité du courant est analogue à la solution étalon, c’est-à-dire que l’intensité du courant est analogue à la normalité ou la molarité dans les utilisations de réactifs
classiques, et le temps est analogue au volume analysé.
En coulométrie, ce n’est plus une micro-électrolyse comme en voltamétrie, on va
transformer toute la substance.
La quantité d’électricité consommée va être proportionnelle à la concentration du produit à doser en solution.
La méthode coulométrique pour être applicable, il faut que la quantité d’électricité mesurée corresponde exactement à la substance, il ne faut pas d’autres substances à côté.
Il faut aussi bien contrôler les conditions opératoires, on contrôle soit l’intensité du courant, soit le potentiel de
l’électrode.
Il faudra ensuite mettre en évidence le point d’équivalence de la réaction, et au final déterminer la quantité d’électricité mise en jeux.
Example : la réduction de: Fe3+ + 1e- ↔ Fe2+
Si on utilise un courant de 10-3A pendant 100s, la quantité d’électricité est Q = 10-3 x 102 = 10-1C.
Pour arriver à savoir quelle quantité de substance de Fe3+ s’est transformée : On appliquant la loi de Faraday mFe3+ = (A/nF).Q
(A est la masse atomique de Fe3+) avec Q = i.t; mFe3+ =
(55.84/1×96500) 10-1 = 57.86 µg qui ont été consommés dans la
réaction.
Coulométrie directe
En coulométrie directe, la quantité de la substance à doser réagit sur une électrode dont le potentiel reste constant par rapport à la solution, tendis que le courant décrois au cours de l’électrolyse.
Donc, il est possible de réduire ou oxyder totalement un composé à l’aide d’une réaction d’électrolyse.
Dans ces conditions, la quantité d’électricité mise en jeu est en fonction de la quantité de la substance oxydée ou réduite.
Coulométrie à potentiel constant
A partir de courbes intensités potentielles d’une réaction d’oxydo- réduction (montage à trois électrodes), on va appliquer un potentiel correspondant au palier de diffusion et on fait passer le courant avec une certaine intensité au début qui va diminuer.
Le tracé (i = f(t)) est une fonction exponentielle et décroissante et la quantité d’électricité est estimée grâce à la relation :
Q = dt
Le potentiel correspond à un point suffisamment éloigné sur le palier de diffusion et la concentration de l’espèce X à l’électrode X(0, t) s’annule très rapidement.

-Montage à trois électrodes – Courbes de polarisations
Le courant s’annule lorsque la réaction est terminée.
Ce dosage nécessite théoriquement la détermination de la quantité d’électricité consommée, celle-ci peut se réaliser de deux façons :
Mettre en série un système de mesure de cette quantité (intégrateur)
En traçant la courbe représentant la décroissance de l’intensité de courant en fonction du temps et en mesure la surface comprise entre la courbe et les deux axes
Coulométrie à intensité constante
Dans ce cas, le courant va jouer le rôle de burette coulométrique, on introduit une quantité de courant qui va transformer un réactif titrant qui sera généré.
L’intensité étant fixe, le potentiel enregistré reste constant tant qu’il reste sur l’électrode du métal à oxydé ou à réduire.
Dès que la dernière trace du métal a disparu le potentiel va brusquement varier et ce fixe à une valeur correspondant à l’oxydation du solvant.
L’intensité du courant est constante au cours de l’électrolyse et la quantité d’électricité mise en œuvre est proportionnelle au temps pendant la quelle le potentiel est maintenu constant.
V
Variation du potentiel lors d’une
électrolyse à intensité constante
t
t0 tf
Titrage coulométrique indirecte (coulométrie indirecte) Considérant le dosage d’un composé X susceptible de réagir sur l’ion métallique M+ suivant la réaction : M+ + X- → MX
Donc, il est possible de préparer M+ par oxydation du métal suivant la réaction :
M → M+ + 1e-
et l’ion M+ va réagir avec X- pour donner MX
Supposant que la totalité de la substance X- a été transformée en MX.
La quantité d’électricité mise en jeu pour préparer la quantité nécessaire de réactif M+ au sien de du milieu réactionnel à partir de la substance M et en fonction de la quantité de X- initialement présent dans le milieu.
Il suffit alors de disposer d’un système permettant de mettre en évidence le point équivalent correspond à la réaction chimique précédente
Exemples : 1/Dosage des halogénures
Utilisation d’une électrode d’argent qui va pouvoir générer des ions Ag+.
Ag0 → Ag+ + 1e-, Ag+ + X- → AgX↓ 2/ Dosage acide-base
On peut utiliser l’eau en réduction pour générer des ions OH- quantitativement par rapport à la quantité d’électricité mise en jeu.
Si on génère des ions OH-, on pourra doser des solutions acides.
On peut également enlever des protons à la solution.
Même chose en oxydation, si on oxyde l’eau, on produit des ions H+ et l’on pourra doser des solutions alcalines.
Réduction 2H2O + 2e- → H2↑ + 2OH- acidimétrie
2H+ + 2e- → H2↑
Oxydation 2H2O → O2 + 4H+ + 4e- alcalinimétrie
4OH- ↔ O2 + 2H2O + 4e-
3/ Dosage par bromuration
2Br- → Br2 + 2e- Réaction d’oxydation.
Le Br2 formé pourra se fixer sur des substances comme les phénols (oxyquinol), les
dérivés aminés.
4/ Dosage en iodométrie
3I- → I3- + 2e- On peut utiliser ceci dans le dosage de Karl Fisher.
La méthode de Karl Fischer : est une méthode chimique de mesure de la teneuren eau d’un échantillon par titrage.
La procédure est basée sur l’oxydation du dioxyde de soufre par le diiode
SO2 + I2 + 2 H2O ↔ H2SO4 + 2 HI.

Conductimétrie
Conduction de l’électricité d’une solution
Le caractère conducteur de l’électricité, d’une solution, est uniquement dû aux ions qu’elle contient.
Une solution qui contient des ions est appelée ” solution électrolytique.
En l’absence d’ions, un liquide ne conduit quasiment pas le courant électrique : c’est quasiment un isolant.
Pour qu’une solution électrolytique soit traversée par un courant électrique, il faut plonger deux électrodes conductrices dans la solution et leur appliquer une tension électrique.
Dans une solution électrolytique traversée par un courant continu:
les cations (ou ions positifs) migrent vers l’électrode reliée au pôle négatif.
les anions (ou ions négatifs) migrent vers l’électrode reliée au pôle positif.
La loi d’ohm relative à un conducteur métallique homogène se traduit par: U = R.I.
La résistance d’un matériau dépend de la nature et des dimensions du conducteur.
Elle est d’autant plus grande que la longueur est grande, et que la section est faible.
Conductance d’une portion de solution
L’expérience montre que si l’on applique une tension alternative sinusoïdale, de valeur efficace U, entre deux électrodes situées en regard, plongeant dans une solution aqueuse électrolytique « suffisamment diluée », elle est alors parcourue par un courant alternatif sinusoïdal de valeur efficace I proportionnelle à U:
I = G.U donc G = 1/R
Le coefficient G est appelé conductance de la portion de solution comprise entre les deux électrodes en regard (figure précédente pour laquelle les électrodes en regard sont des plaques métalliques de forme rectangulaire).
La conductance G caractérise l’aptitude de la portion de solution à conduire le courant électrique.
L’ensemble des deux plaques rectangulaires en regard s’appelle ” cellule conductimétrique”.
Unités internationales G = I/U G est en siemens (S) quand I est en ampère (A) et U est en Volt (V).
On appelle “résistance” d’une portion de solution, la grandeur notée R, égale à l’inverse de la conductance R = 1/G où R est exprimée en ohm (Ω) quand G est exprimée en siemens (S).
Montage de mesure d’une conductance, il comprend :
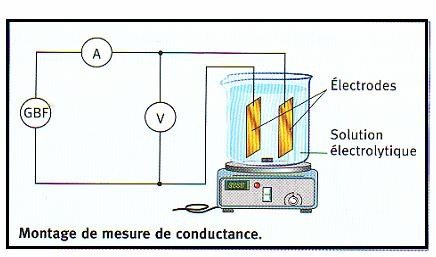
Densité de courant qui traverse l’électrolyseur
Tous les ions qui traversent la solution entre deux électrodes par seconde seront compris dans un cylindre de section S et d’une hauteur égale à la vitesse :
v- = U-.E (pour l’anion), v+ = U+.E, (U-, U+ sont la mobilité du l’anion et du cation)
donc dans un volume V(cm3) = S.U-.E ( la mobilité en cm2/volts)
(S.U-.E.
C.10-3) = neq (nombre d’équivalent gramme)
I- = neq.
F = S.U-.E.
C.10-3 .F I+= neq.
F = S.U+.E.
C.10-3 .F
Ou F est le Faraday (96500 coulombs)
Pour un électrolyte binaire fort l’intensité de courant est :
I = I+ + I- = S.
E.
C.10-3 .F (U+ + U-)
i = I/S = E.
C.10-3 .F (U+ + U-)
Exemple : Un mélange de deux électrolytes, NaCl(C1M), FeCl3 (C2 M)
i = 10-3.F.E (UNa+C1 + 3C2UFe3+ + UCl-C1 + 3UCl- C2)
Dans le cas général : i = F.E 10-3
Pour un électrolyte faible la densité de courant est :
i = F.E.α.10-3
Conductivité d’une solution électrolytique
On utilise par définition, le mot résistance pour un électrolyte comme un métal et par conséquent la résistance spécifique ou la résistivité ρ (Ohm.cm) comme la résistivité d’une colonne d’électrolyte de section 1 cm2 et de longueur 1 cm avec un champ uniforme.
Pour un électrolyte, on utilise souvent l’inverse de la résistivité
λ = 1/ρ
C’est la conductivité spécifique elle est donnée en Ohm-1.cm-1 On a R = ρL/S ; U = RI ; implique que U = (L/ λS).I
La densité de courant i = I/S et le champ électrique E = U/L
Donc i = λ E
D’après l’équation densité de courant précédente, la conductivité
λ = i/E = F.10-3
Pour un électrolyte binaire :
λ = F.10-3 C (U+ + U-) Relation de Cohlrausch
Conductivité équivalente
Suivant la relation précédente de la conductivité, λ varie en fonction de la concentration et s’annule lorsque C→0 c-à-d en absence d’électrolyte.
On appelle une conductivité équivalente la quantité :
Λ = 103 λ/Ceq Ceq en équivalent-gramme/L La relation de Cohlrausch peut s’écrire :
Λ = F. (U+ + U-) pour un électrolyte fort
Λ = F. α.(U+ + U-) pour un électrolyte faible
La représentation graphique de Λ = f( ) peut classer les électrolytes
en deux catégories :
Les électrolytes forts, pour les quels les courbes sont presque linéaire alors que les électrolytes faibles pour les quels les courbes représentent des courbures même aux faibles concentrations
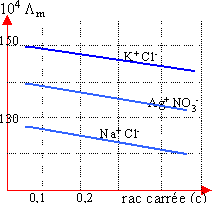
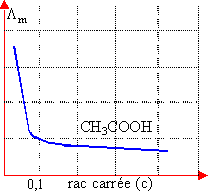
Electrolytes fort Electrolyte faible
Pour les électrolytes forts, on peut facilement déterminer la conductivité équivalente limite Λ∞ lorsque Ceq→0 suivant cette relation : Λ = Λ∞ – a a est une constante qui dépendant de la
nature du solvant.
– pour un électrolyte faible, la détermination de Λ∞ par extrapolation sur la courbe est infiniment moins sur que pour un électrolyte fort alors :
Λ = F.α.(U+ + U-)
Α obéit à la loi de dilution d’OSTWERD
[C.α2/(1- α)] = K quand C→= 0 α →1
Donc Λ∞ = F. (U+ + U= λs-o)l
On déduit α = Λ/Λ∞
On remplaçant dans l’équation d’OSTWERD
CΛ = K Λ 2/Λ – K Λ
∞ ∞
Avec cette relation on peut tracer la droite CΛ = f( 1/Λ) et on détermine
K et Λ∞
La conductivité équivalente d’une solution Λsol =
où est la conductivité équivalente ionique.
On a aussi Λ = 103 λ/Ceq, pour une solution
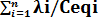
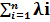
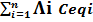
-3
=
= 10
=λsol
=103
C’est la conductivité spécifique d’une solution de n ions
Titrage conductimétrique
Le dosage conductimétrique est basé sur la variation de la conductivité λ d’une solution électrolytique lors d’un ajout d’un réactif susceptible de réagir sur cette solution
Exemple :
– dosage acido-basique:
(H+ + OH- ↔ H2O)
-dosage par précipitation
(KCl + AgNO3 ↔ K+ + AgCl + NO3-)
Généralement, le titrage s’effectue en utilisant un réactif 10 à 20 %
plus concentré que la solution à doser de façon à ce qu’on néglige la dilution.
Une fois le point équivalent est atteint, la variation de la conductivité est du à l’excès du réactif
Formes des courbes de titrage
A/ Dosage d’une solution d’électrolyte fort par un électrolyte fort
Ex: HCl + NaOH ↔ H2O + Na+ + Cl–
B/ Dosage d’un électrolyte faible par un réactif fort
Ex : CH3COOH + KOH ↔ CH3COO- + H2O + K+
C/ Dosage d’un électrolyte fort qui provient d’un acide faible plus un
réactif fort
Courbes
Ex : CH3COONa + HCl ↔ CH3COO– + Cl– + Na+
C
B
A
Volume (mL)
λ (mS.cm-1)
VI-5- Applications pharmaceutiques
Les mesures des quantités de matière ont une importance capitale dans le domaine de la santé.
Elles donnent lieu à de nombreuses analyses comme celles de certaines espèces chimiques contenues dans le sang.
Si la valeur de leur concentration n’est pas comprise dans un intervalle donné, une pathologie est alors détectée.
Ex: Chlorure de sodium dans le sérum et autres
| Espèce analysée | Normes de concentration molaires (mmol.L-1) |
| Calcium | 2, 25 – 2,5 |
| Chlorure | 95 – 105 |
| Sodium | 135-150 |
| Potassium | 3,5-5,5 |
| Magnésium | 0,75 – 1 |
| Phosphore | 0,8 – 1, 35 |
| Bicarbonates | 22 – 30 |
| Fer | 10 à 30μmol |
| Glucose | 3,6 à 5,5 |
| Protéines totales | 65 à 75 g/l |
| Urée | 3 à 8 |
| Créatinine | 0,053 à 0,115 |
| Glycémie à jeun | 4,45 à 6,40 |
| Cholestérol total | 4,00 à 6,50 |
| Triglycérides | 0,34 à 1,70 |
| Cholestérol HDL | 1,00 à 1,95 |
On donne les informations suivantes :
l’urée a pour formule OC(NH2)2 ;
la créatine ou acide méthylguanidino-acétique est une substance
azotée ; c’est un produit intermédiaire du métabolisme des protides ; elle est transformée en créatinine par réaction interne ;
la glycémie représente le taux de glucose dans le sang (l’augmentation de la glycémie, hyperglycémie, est le signe essentiel du diabète) ; la formule semi-développée du glucose est :
HOCH2–CHOH–CHOH–CHOH–CHOH–CHO
le cholestérol est une molécule complexe de formule brute C27H45OH le cholestérol HDL (high density lipoprotéins), de même formule brute C27H45OH, aide à la protection des vaisseaux ;
les triglycérides sont des triesters du glycérol (ils représentent 95 %
des corps gras).
La masse molaire moyenne des triglycérides rencontrés dans le sang est : M = 887 g.mol–1.
Exemple : élimination de Plomb et cadmium
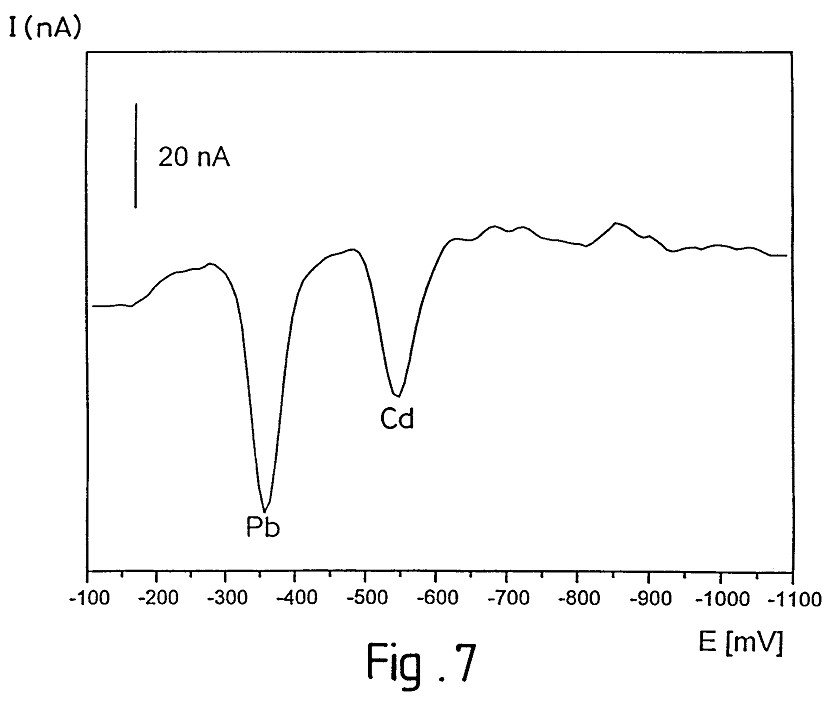
Microcapteurs et microsystèmes électrochimiques intégrés fiables pour l’analyse chimique directe de composés en milieux aqueux complexes
Microcapteur pour mesures électrochimiques permettant de déterminer dans un milieu aqueux la concentration ou le gradient de concentration d’au

oins un composé chimique de faible taille ou masse
m
m o m (
d
m
é
m
oléculaire sous forme organique, minérale, neutre u ionique, comprenant un réseau (15) de icroélectrodes (16), conformé sur une plaquette
10) supportée par un substrat isolant (7), et relié à un contact permettant de le connecter à un appareil e mesure par au moins un conducteur protégé par un revêtement isolant, caractérisé en ce que le dit
icrocapteur est totalement recouvert par un gel hydrophile (25) inerte vis-à-vis du composé chimique, ayant un taux d’hydratation d’au moins 70 % et une paisseur d’au moins 10 fois supérieure à la taille des
icroélectrodes (16), et microsystème électrochimique intégré le comprenant.
microélectrodes gel hydrophile
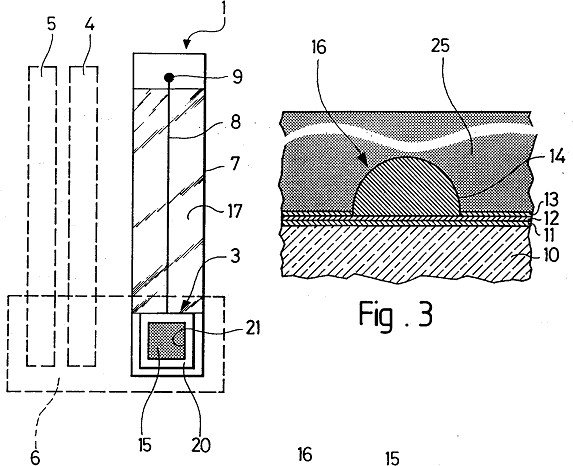
dépôt de mercure
une plaquette
un substrat (7) isolant,
une électrode auxiliaire en Ir
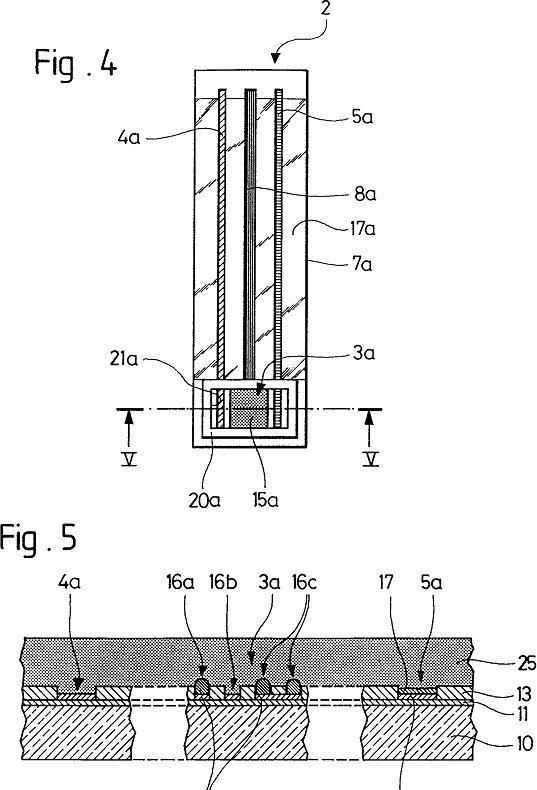
une électrode de référence Ir/lr02 conducteurs 8a recouvert d’un revêtement isolant 17a
revêtement isolant (1 7, 17a),
microélectrodes (16), de façon individuelle (16a, 16b) ou par groupes (16c),